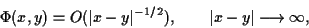Scattering Theory - An Overview
Scattering theory is concerned with the effect obstacles or inhomogeneities
have on an incident waves. There are two types of problems in this area:
- The Direct Problem: This problem is concerned with determining
the scattered field from the knowledge of the incident field and
the scattering obstacle.
- The Inverse Problem: Here one tries to determine the shape and/or
physical properties of the scatterer from the measurement of the
scattered field for a number of incident fields.
The propagation of waves in a homogeneous, isotropic medium is mathematically
described by the wave equation,
where c denotes the speed of propagation. In the Brunel Rough Surface
Scattering group, we are concerned with scattering problems involving
time harmonic waves, i.e. wave fields of the form
where w denotes the circular frequency. Such
wave fields are important for many applications in acoustics,
electro-magnetic or elasticity theory. The wave equation can then be
reducted to the Helmholtz equation,
where k = w/ c.
Direct Scattering Problems
Scattering by a bounded obstacle
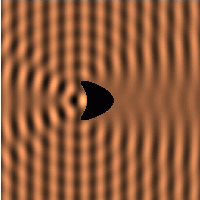
The total field is usually represented as the sum of the incident and
the scattered field. The scattering problem can then be formulated as a
boundary value problem for the scattered field in the region outside
the scattering obstacle, consisting of
- the Helmholtz equation,
- a boundary condition on the boundary of the scattering obstacle,
- Sommerfeld's radiation condition.
As the boundary condition either a Dirichlet, Neumann or Robin boundary
condition is possible. In acoustics, these correspond to sound soft, sound hard
or impedance surfaces of the obstacle. Sommerfeld's raditation condition is
uniformly in all directions x/r, where us denotes the
scattered field and m = 2,3 the spacial dimension of the problem.
The image above is a visualisation of the scattered field for such a bounded
obstacle problem. A plane wave is incident from the left-hand side and scattered by
the kite-shaped object. A Dirichlet boundary condition (i.e. the total field
vanishes) was used on the surface. For more detail on this problem, there is a
separate page including an animation (Java applet) of the wave
field.
Scattering by a diffraction grating

A diffraction grating is a very simple type of unbounded scatterer: It is a surface
that is invariant in the, say x3 coordinate direction while showing
some periodicity in the x1 direction. If the incident field is also
constant in the x3 direction, the scattering problem can be treated as a
2-dimensional problem. The diffraction grating can then be described as the graph of a
function f that is periodic with, say, period L.
If the incident field also is periodic with a certain, possibly different, period
(which is the case for an incident plane wave!), both the incident and the scattered
field will be quasi-periodic. This property allows substantial simplifications
as the problem can thus be dealt with in spaces of periodic functions.
A further difficulty arises, in that the scattered field in a diffraction problem
will, in general, not show any decay in directions parallel to the surface. Thus,
Sommerfeld's radiation condition will not apply. It is replaced by the Rayleigh
Expansion Radiation Condition (RERC), that the scattered field has, at some height
above the surface, an expansion in plane waves propagating upwards and evanescent waves,
decaying exponentially with distance from the surface.
Numerically, the problem can be treated, for example, by a boundary integral ansatz with
a Nyström method for the numerical treatment of the resulting boundary integral
equation. This type of method is extremely efficient, and a code developed by the Brunel
Rough Surface Scattering group clearly demonstrates the theoretically expected exponential
convergence rates. There is also a more detailed description of the
problem available, that includes an animation of the total field based on a Java applet.
Scattering by a rough surface
Of special interest to the Brunel Rough Surface Scattering group
are problems involving effectively unbounded obstacles. Such an
obstacle is termed a rough surface, if it can be represented as
the graph of a bounded, continuous function f. Often,
f will be required to satisfy some additional smoothness
properties, usually Lipschitz continuity of its first derivative.
A number of difficulties arise when dealing with such problems.
Firstly, to formulate the problem as a boundary value problem,
a suitable radiation condition has to be imposed. Such a condition
is the upward propagating radiation
condition introduced by
Chandler-Wilde.
It was shown that this
radiation condition ensures uniqueness of solution to the sound soft
and impedance surface scattering problems for quite general classes
of incident fields, including cylindrical and plane waves.
Secondly, when deriving boundary integral equation formulations,
the standard fundamental solution, i.e. the Green's function in free
field conditions, turns out to be poor choice as the kernel in
single- and double-layer potentials. This is due to the fact that
we cannot expect the surface density to be decaying along the
infinite surface for general classes of incident waves. Thus,
the decay rate of the free field Green's function, i.e.
is not enough to ensure existence of the boundary integral for surface
densities that are merely bounded. Thus one has to turn to alternatives,
for example the Greens function G(x,y) for a half plane with
Dirichlet boundary conditions. This function shows the decay rate
Thus, for a scattering surface f, bounded in
x2-direction, the boundary integrals exist, even
if the density is merely bounded.
However, and this is a further difficulty, the arising integral
operators have an unbounded range of integration. Even for the simplest
case, a convolution operator, one observes that such an operator
is not compact. Thus, an entirely new solvability theory is required
to prove that the boundary integral equation admits a unique solution.
The extension of these results to the full, 3-dimensional case, is
the object of much ongoing research in the Brunel Rough Surface
Scattering group.
Elastic Wave Scattering
If one considers the propagation of waves in an elastic solid, very
similar types of scattering problems occur. However, even in the simplest
case of an isotropic, homogeneous medium of propagation, the elastic
wave motion is much more complicated than in the acoustic or electro-magnetic
case. This is due to the fact that there are two types of waves,
compressional (P) and shear (S) waves, that propagate
through the medium at different wave speeds cp and
cs, respectively. These two wave types are coupled
through the boundary conditions: even a plane P-wave incident onto
a planar surface will give rise to both a reflected P- and S-wave, with
different directions of propagation.
In an isotropic, homogeneous medium, the wave motion of time-harmonic
fields is described by the Navier equation,
where m, l
(m > 0, m +
l > 0) denote the
Lame constants and and w > 0 the
circular frequency. This equation can be considered in either two or
three dimensions.
The investigation of the above three types of scattering problems is
also possible via boundary integral equation methods. For the bounded
obstacle case, these methods are well-known, while the first proofs
of well-posedness of the boundary integral equation formulations
for diffraction grating problems or rough surfaces can be found
in some of the author's papers.
Inverse Scattering Problems
Inverse problems are problems of reconstruction of parameters
in a mathematical problems from (partial) knowledge of the problems
solution. An examples is the reconstruction of coefficients
in a PDE from knowledge of the Cauchy Data of the solution on the
boundary of the domain. Such problems are allmost always non-linear
and ill-posed. Thus they require regularisation methods for
their solution.
Reconstruction of a bounded obstacle
An inverse scattering problem consists in the reconstruction
of a scattering obstacle from the knowledge of the far-field data
for one or a number of incident fields. There are currently three
methods available for the solution of such a problem:
- iterative methods relying on a Newton type iteration,
- methods splitting up the problem in the ill-posed linear
problem of reconstructing the scattered field from the
far-field pattern and the well-posed non-linear problem
of finding the boundary from the scattered field,
- methods using a direct characterisation of the obstacle.
References
Books
- D. Colton and R. Kress, Integral Equation Methods in Scattering Theory,
Wiley, 1983.
- D. Colton and R. Kress, Inverse Acoustic and Electromagnetic Scattering
Theory, 2nd edition, Springer-Verlag, 1998.
- A. Kirsch, An Introduction to the Mathematical Theory of Inverse Problems,
Springer-Verlag, 1996.
Papers by members of the Brunel group
The following members of the Brunel Rough Surface Scattering group maintain a list of
their publications on separate pages:
Other Resources
- There are some nice examples of scattering problems and related numerical methods on
the home page of Klaus
Giebermann at Bonn University.
Page written and maintained by Tilo
Arens
last change: 5 January 2001
Mathematical formulae by latex2html